internal_rax
Redis RAX radix tree
 Redis Internel Course
Redis Internel Course
|
 Redis Technical Support
Redis Technical Support
|
 Redis Enterprise Server
Redis Enterprise Server
|
|---|
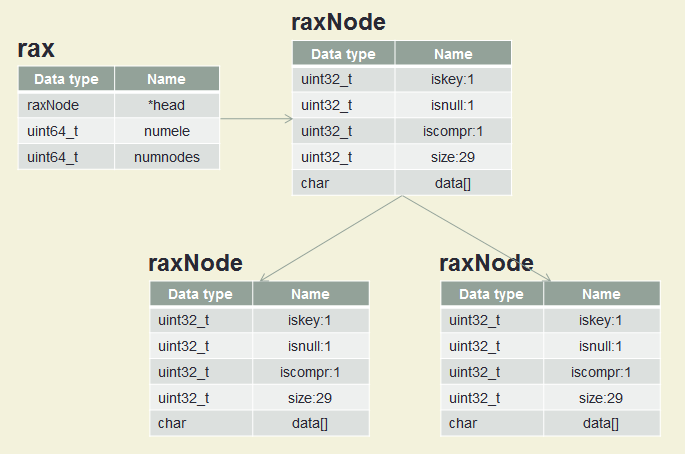
RAX radix tree
기본 데이터 구조
| Data Type | Name | Size | Description |
|---|---|---|---|
| raxNode | *head | 8 bytes | Head raxNode 포인터 |
| uint64_t | numele | 8 bytes | element 개수 |
| uint64_t | numnodes | 8 bytes | 노드 개수 |
| Data Type | Name | Size | Description |
|---|---|---|---|
| uint32_t | iskey:1 | 1 bit | 1이면 key 0이면 key 아님 |
| uint32_t | isnull:1 | 1 bit | 1이면 value pointer 없음 1이면 value pointer 있음 |
| uint32_t | iscompr:1 | 1 bit | 1이면 압축(자식 노드 1개) 노드 0이면 일반(자식 노드 n개) 노드 |
| uint32_t | size:29 | 29 bits | 문자열 길이 |
| char | date[] | ? bytes | 데이터 |
API
- raxInsert(): 저장
int raxInsert(rax *rax, unsigned char *s, size_t len, void *data, void **old)- Stream: rax -> key, s -> id, data -> listpack(field,value) pointer
- ACL: rax -> Users, s -> username, data -> user pointer
ACL에서 username으로 사용자 정보를 저장/조회할 때 사용한다. 예) acl setuser username - Cluster: rax -> slots_to_keys, s -> key, data -> NULL
클러스터에서 슬롯별로 키를 관리하는데 사용한다. 예) cluster getkeysinslot <slotnum> - Client: rax -> clients_index, s -> client id, data -> client pointer
Client id를 rax에 저장해 놓고 id로 client를 찾을 때 사용한다. 예) client unblock <id>
- raxRemove(): 삭제
int raxRemove(rax *rax, unsigned char *s, size_t len, void **old) - raxFind(): 같은 키 찾기
void *raxFind(rax *rax, unsigned char *s, size_t len) - raxFree(): Rax 구조체 메모리 해제
void raxFree(rax *rax): 내부에서 raxRecursiveFree()를 호출해서 모든 node 메모리를 해제한다. - raxStart(): 찾기 초기 설정
void raxStart(raxIterator *it, rax *rt) - raxSeek(): 위치 찾기
int raxSeek(raxIterator *it, const char *op, unsigned char *ele, size_t len)
op는 ele를 기준으로 ^(처음 데이터), $(마지막 데이터), >=, <= 등이 사용한다. - raxNext(): 다음
int raxNext(raxIterator *it) - raxPrev(): 이전
int raxPrev(raxIterator *it) - raxStop(): 찾기 종료
void raxStop(raxIterator *it)
Internal API
- raxSetData(): 데이터(value) 저장
void raxSetData(raxNode *n, void *data) - raxGetData(): 데이터(value) 조회
void *raxGetData(raxNode *n) - raxLowWalk(): 위치(insert, split) 찾기
static inline size_t raxLowWalk(rax *rax, unsigned char *s, size_t len, raxNode **stopnode, raxNode ***plink, int *splitpos, raxStack *ts) - raxAddChild()
raxNode *raxAddChild(raxNode *n, unsigned char c, raxNode **childptr, raxNode ***parentlink) - raxRemoveChild()
raxNode *raxRemoveChild(raxNode *parent, raxNode *child)
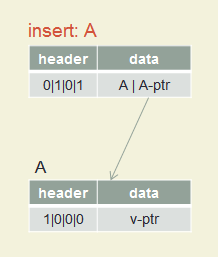
Radix Tree: Insert Example
RAX Data Structure
| Name | Description |
|---|---|
| iskey | 1: key이면, 0: key가 아니면 |
| isnull | 1: value pointer가 없음, 0: value pointer가 있음 |
| iscompr | 1: 압축(자식 노드 1개) 노드, 0: 일반(자식 노드 n개) 노드 |
| size | 문자열 길이 |
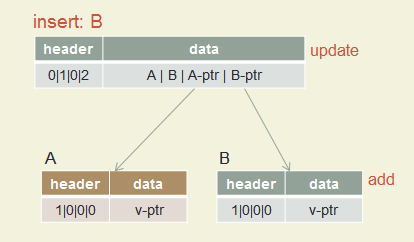
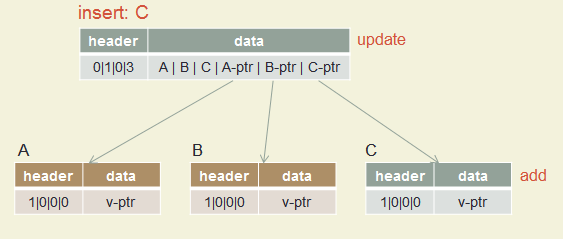
Insert A, B, C
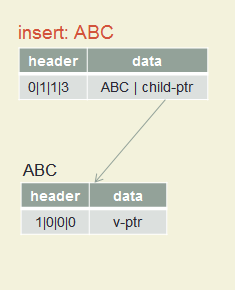
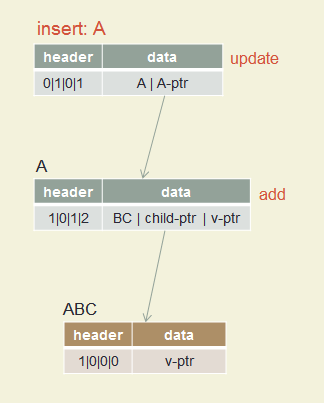
Insert ABC, A
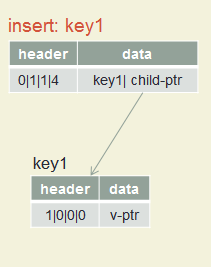
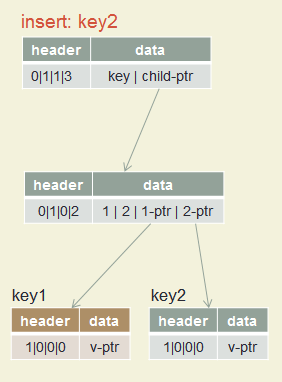
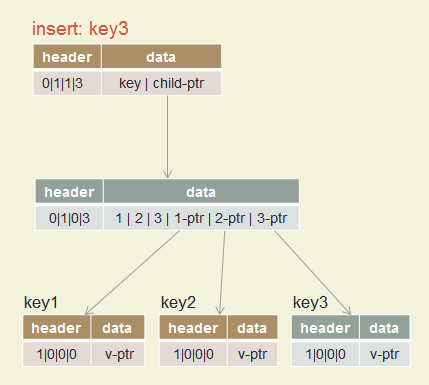
Insert key1, key2, key3
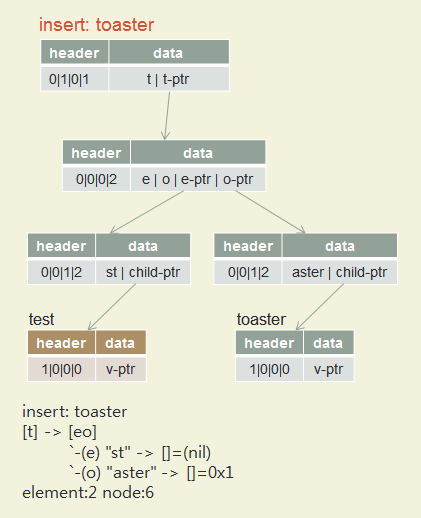
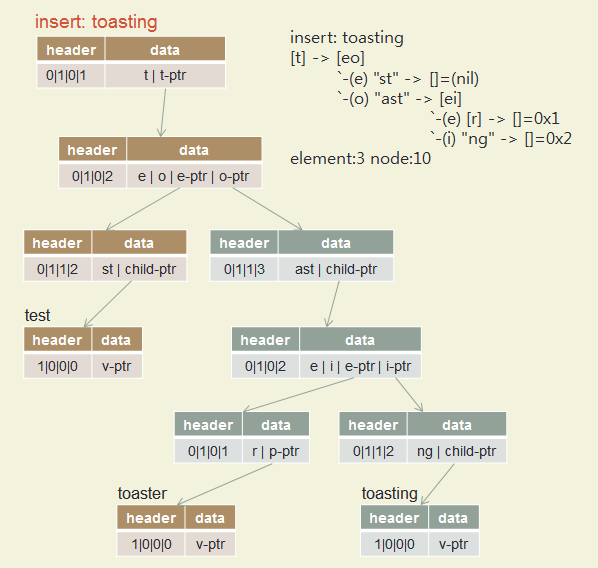
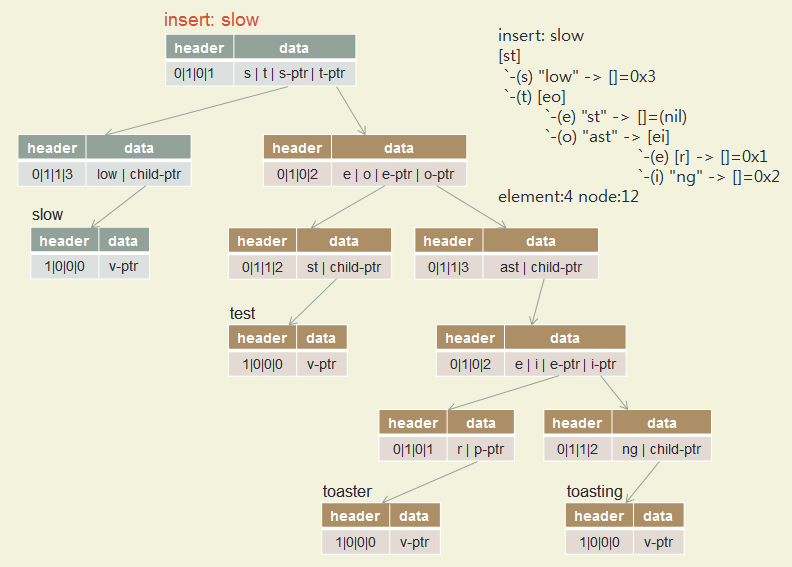
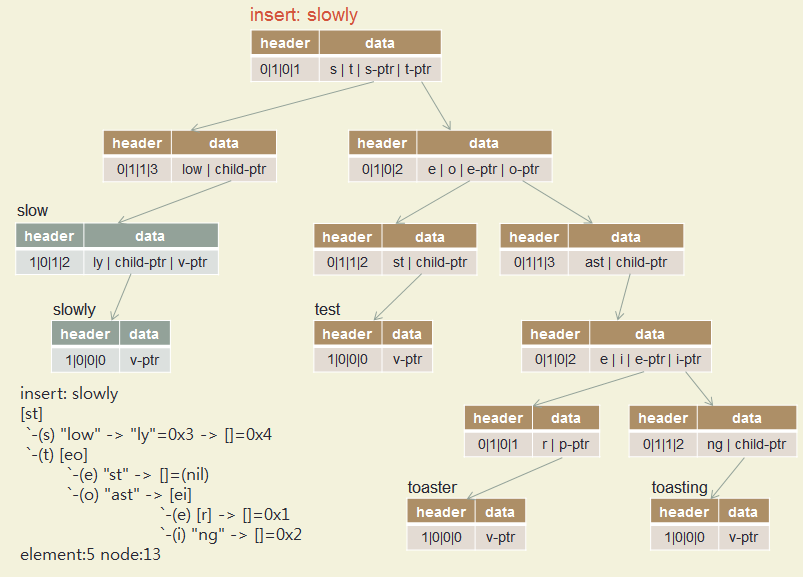
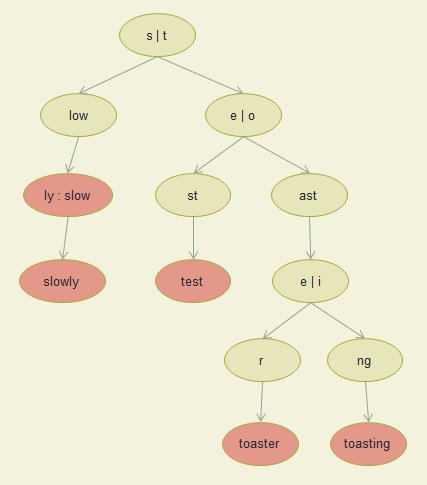
Insert test, toaster, toasting, slow, slowly

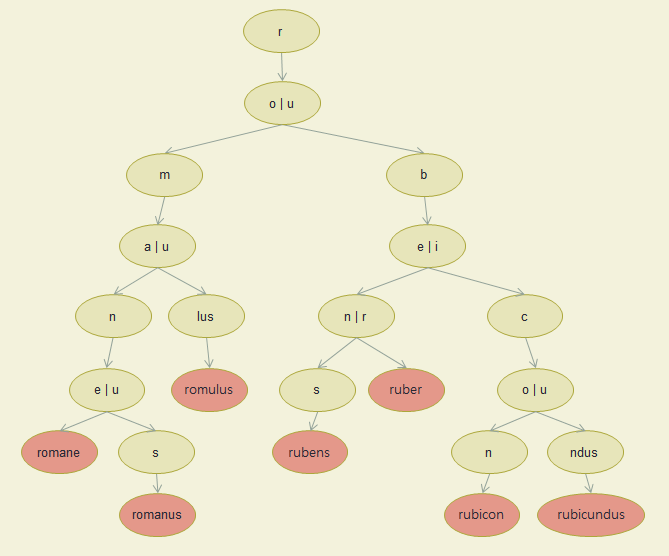
Insert romane ... rubicundus
- romane
- romanus
- romulus
- rubens
- ruber
- rubicon
- rubicundus

Rax, an ANSI C radix tree implementation
출처:
https://github.com/antirez/rax
Rax is a radix tree implementation initially written to be used in a specific place of Redis in order to solve a performance problem, but immediately converted into a stand alone project to make it reusable for Redis itself, outside the initial intended application, and for other projects as well.
Rax는 기수 트리(radix tree)로 레디스 성능 문제를 해결하기 위해서 개발되었습니다. 이제 레디스 자체뿐만이 아니라 다른 프로젝트에서도 사용될 수 있도록 독립 프로젝트로 변환했습니다.
The primary goal was to find a suitable balance between performances and memory usage, while providing a fully featured implementation of radix trees that can cope with many different requirements.
주요 목표는 성능과 메모리 사용간에 적절한 균현을 찾는 동시에 다양한 요구 사항에 대처할 수 있는 완전한 기능의 기수 트리를 구현해서 제공하는데 있습니다.
During the development of this library, while getting more and more excited about how practical and applicable radix trees are, I was very surprised to see how hard it is to write a robust implementation, especially of a fully featured radix tree with a flexible iterator. A lot of things can go wrong in node splitting, merging, and various edge cases. For this reason a major goal of the project is to provide a stable and battle tested implementation for people to use and in order to share bug fixes. The project relies a lot on fuzz testing techniques in order to explore not just all the lines of code the project is composed of, but a large amount of possible states.
이 라이브러리를 개발하는 동안 실용적이고 적용 가능한 기수 트리가 얼마나 많은지에 대해 점점 더 흥분하게되었지만, 특히 유연한 반복기가 있는 완전한 기능을 갖춘 기수 트리의 강력한 구현을 작성하는 것이 얼마나 어려운지 매우 놀랐습니다. 노드 분할, 병합 및 다양한 엣지 케이스에서 많은 일이 잘못 될 수 있습니다. 이러한 이유로 이 프로젝트의 주요 목표는 사람들이 버그 수정을 공유하고 사용할 수 있도록 안정적이고 전투 테스트를 거친 구현을 제공하는 것입니다. 이 프로젝트는 퍼지 테스트 기술에 의존하여 프로젝트가 구성된 모든 코드 라인뿐만 아니라 가능한 많은 상태를 탐색합니다.
Rax is an open source project, released under the BSD two clause license.
Rax는 오픈 소스 프로젝트이며 BSD 2 조항 라이센스로 배포됩니다.
Major features: 주요 특징.Fast lookups: 빠른 조회
Complete implementation: 완전한 구현
Readable and fixable implementation: 가독성있고 유연한 구현
Portable implementation: 이식성있는 구현
Extensive code and possible states test coverage using fuzz testing.
광범위한 코드 및 가능한 상태는 퍼지 테스트를 사용하여 적용 범위를 테스트합니다.
The layout of a node is as follows. In the example, a node which represents a key (so has a data pointer associated), has three children x, y, z. Every space represents a byte in the diagram.
노드의 레이아웃은 다음과 같습니다. 이 예에서 키를 나타내는 노드(데이터 포인터가 연결되어 있음)에는 세 개의 자식 x,y,z가 있습니다. 다이어그램에서 모든 space는 바이트를 나타냅니다.
The header HDR is actually a bitfield with the following fields:
헤더 HDR은 실제로 다음 필드가 있는 비트 필드입니다.
Compressed nodes represent chains of nodes that are not keys and have exactly a single child,
so instead of storing:
압축 노드는 키가 아니고 정확히 하나의 자식을 갖는 노드 체인을 나타내므로 다음과 같이 저장하지 않고:
We store a compressed node in the form:
압축 노드를 다음 형식으로 저장합니다.
The layout of a compressed node is:
압축 노드의 레이아웃은 다음과 같습니다.
Rax is a radix tree implementation initially written to be used in a specific place of Redis in order to solve a performance problem, but immediately converted into a stand alone project to make it reusable for Redis itself, outside the initial intended application, and for other projects as well.
Rax는 기수 트리(radix tree)로 레디스 성능 문제를 해결하기 위해서 개발되었습니다. 이제 레디스 자체뿐만이 아니라 다른 프로젝트에서도 사용될 수 있도록 독립 프로젝트로 변환했습니다.
The primary goal was to find a suitable balance between performances and memory usage, while providing a fully featured implementation of radix trees that can cope with many different requirements.
주요 목표는 성능과 메모리 사용간에 적절한 균현을 찾는 동시에 다양한 요구 사항에 대처할 수 있는 완전한 기능의 기수 트리를 구현해서 제공하는데 있습니다.
During the development of this library, while getting more and more excited about how practical and applicable radix trees are, I was very surprised to see how hard it is to write a robust implementation, especially of a fully featured radix tree with a flexible iterator. A lot of things can go wrong in node splitting, merging, and various edge cases. For this reason a major goal of the project is to provide a stable and battle tested implementation for people to use and in order to share bug fixes. The project relies a lot on fuzz testing techniques in order to explore not just all the lines of code the project is composed of, but a large amount of possible states.
이 라이브러리를 개발하는 동안 실용적이고 적용 가능한 기수 트리가 얼마나 많은지에 대해 점점 더 흥분하게되었지만, 특히 유연한 반복기가 있는 완전한 기능을 갖춘 기수 트리의 강력한 구현을 작성하는 것이 얼마나 어려운지 매우 놀랐습니다. 노드 분할, 병합 및 다양한 엣지 케이스에서 많은 일이 잘못 될 수 있습니다. 이러한 이유로 이 프로젝트의 주요 목표는 사람들이 버그 수정을 공유하고 사용할 수 있도록 안정적이고 전투 테스트를 거친 구현을 제공하는 것입니다. 이 프로젝트는 퍼지 테스트 기술에 의존하여 프로젝트가 구성된 모든 코드 라인뿐만 아니라 가능한 많은 상태를 탐색합니다.
Rax is an open source project, released under the BSD two clause license.
Rax는 오픈 소스 프로젝트이며 BSD 2 조항 라이센스로 배포됩니다.
Major features: 주요 특징.
- Memory conscious:
- Packed nodes representation.
- Able to avoid storing a NULL pointer inside the node if the key is set to NULL
(there is an isnull bit in the node header).
키가 NULL로 설정된 경우 노드 내에 NULL 포인터를 저장하지 않아도 됩니다 (노드 헤더에 isnull 비트가 있음). - Lack of parent node reference. A stack is used instead when needed.
부모 노드 참조 부족. 필요한 경우 스택이 대신 사용됩니다.
- Edges are stored as arrays of bytes directly in the parent node, no need to access non
useful children while trying to find a match. This translates into less cache misses compared
to other implementations.
가장자리는 부모 노드에 직접 바이트 배열로 저장되므로 일치하지 않는 하위 항목에 액세스 할 필요가 없습니다. 이것은 다른 구현에 비해 캐시 누락이 적습니다. - Cache line friendly scanning of the correct child by storing edges as two separated arrays:
an array of edge chars and one of edge pointers.
가장자리를 두 개의 분리된 배열 (가장자리 문자 배열과 가장자리 포인터 중 하나)로 저장하여 올바른 하위 항목을 캐시에 친숙하게 스캔합니다. ???
- Deletion with nodes re-compression as needed.
필요에 따라 노드를 다시 압축하여 삭제하십시오. - Iterators (including a way to use iterators while the tree is modified).
반복자(트리가 수정되는 동안 반복자를 사용하는 방법 포함). - Random walk iteration. 랜덤 워크 반복.
- Ability to report and resist out of memory: if malloc() returns NULL the API can report
an out of memory error and always leave the tree in a consistent state.
메모리 부족 저항과 보고 기능 : malloc()이 NULL을 반환하면 API는 메모리 부족 오류를 보고 하고 항상 트리를 일관된 상태로 유지할 수 있습니다.
- All complex parts are commented with algorithms details.
모든 복잡한 부분은 소스 코드에 자세한 알고리즘을 설명(주석)합니다. - Debugging messages can be enabled to understand what the implementation is doing when
calling a given function.
지정된 함수를 호출할 때 구현이 수행하는 작업을 이해하기 위해 디버깅 메시지를 사용할 수 있습니다. - Ability to print the radix tree nodes representation as ASCII art.
기수 트리 노드 표현을 ASCII 아트로 인쇄하는 기능.
- Never does unaligned accesses to memory.
메모리에 조정되지 않은 액세스를하지 않습니다. - Written in ANSI C99, no extensions used.
ANSI C99로 작성되었으며 실행파일은 확장자을 사용하지 않았습니다.
광범위한 코드 및 가능한 상태는 퍼지 테스트를 사용하여 적용 범위를 테스트합니다.
- Testing relies a lot on fuzzing in order to explore non trivial states.
테스트는 사소하지 않은 상태를 탐색하기 위해 퍼지에 많이 의존합니다. - Implementation of the dictionary and iterator compared with behavior-equivalent
implementations of simple hash tables and sorted arrays, generating random data and checking
if the two implementations results match.
사전 및 반복자의 구현은 간단한 해시 테이블 및 정렬된 배열의 동작과 동등한 구현과 비교하여 임의의 데이터를 생성하고 두 구현 결과가 일치하는지 확인합니다. - Out of memory condition tests. The implementation is fuzzed with a special allocator
returning NULL at random. The resulting radix tree is tested for consistency.
Redis, the primary target of this implementation, does not use this feature, but the
ability to handle OOM may make this implementation useful where the ability to survive
OOMs is needed.
메모리 부족 상태 테스트 구현은 NULL 무작위로 돌아오는 특별한 할당자로 퍼지됩니다. 결과 기수 트리의 일관성을 테스트합니다. 이 구현의 주요 대상인 Redis는 이 기능을 사용하지 않지만 OOM을 처리하는 기능은 OOM을 생존할 수 있는 기능이 필요한 경우 이 구현을 유용하게 만들 수 있습니다. - Part of Redis: the implementation is stressed significantly in the real world.
Redis의 일부: 구현은 실제 세계에서 크게 강조됩니다.
The layout of a node is as follows. In the example, a node which represents a key (so has a data pointer associated), has three children x, y, z. Every space represents a byte in the diagram.
노드의 레이아웃은 다음과 같습니다. 이 예에서 키를 나타내는 노드(데이터 포인터가 연결되어 있음)에는 세 개의 자식 x,y,z가 있습니다. 다이어그램에서 모든 space는 바이트를 나타냅니다.
+----+---+--------+--------+--------+--------+ |HDR |xyz| x-ptr | y-ptr | z-ptr |dataptr | +----+---+--------+--------+--------+--------+
헤더 HDR은 실제로 다음 필드가 있는 비트 필드입니다.
uint32_t iskey:1; /* Does this node contain a key? */
uint32_t isnull:1; /* Associated value is NULL (don't store it). */
uint32_t iscompr:1; /* Node is compressed. */
uint32_t size:29; /* Number of children, or compressed string len. */
압축 노드는 키가 아니고 정확히 하나의 자식을 갖는 노드 체인을 나타내므로 다음과 같이 저장하지 않고:
A -> B -> C -> [some other node]
압축 노드를 다음 형식으로 저장합니다.
"ABC" -> [some other node]
압축 노드의 레이아웃은 다음과 같습니다.
+----+---+--------+ |HDR |ABC|chld-ptr| +----+---+--------+
Basic API
The basic API is a trivial dictionary where you can add or remove elements.
The only notable difference is that the insert and remove APIs also accept an optional
argument in order to return, by reference, the old value stored at a key when it is
updated (on insert) or removed.
In order to insert a new key, the following function is used:
Example usage:
The function returns 1 if the key was inserted correctly, or 0 if the key was already
in the radix tree: in this case, the value is updated. The value of 0 is also returned
on out of memory, however in that case errno is set to ENOMEM.
If the associated value data is NULL, the node where the key is stored does not use additional memory to store the NULL value, so dictionaries composed of just keys are memory efficient if you use NULL as associated value.
Note that keys are unsigned arrays of chars and you need to specify the length: Rax is binary safe, so the key can be anything.
The insertion function is also available in a variant that will not overwrite the existing key value if any:
The function is exactly the same as raxInsert(), however if the key exists the function
returns 0 (like raxInsert) without touching the old value. The old value can be still
returned via the 'old' pointer by reference.
This function returns the special value raxNotFound if the key you are trying to access is
not there, so an example usage is the following:
raxFind() is a read only function so no out of memory conditions are possible,
the function never fails.
The function returns 1 if the key gets deleted, or 0 if the key was not there.
This function also does not fail for out of memory, however if there is an out of memory
condition while a key is being deleted, the resulting tree nodes may not get re-compressed
even if possible: the radix tree may be less efficiently encoded in this case.
The old argument is optional, if passed will be set to the key associated value if the function successfully finds and removes the key.
Creating a radix tree and adding a key
A new radix tree is created with:
rax *rt = raxNew();
int raxInsert(rax *rax, unsigned char *s, size_t len, void *data,
void **old);
Example usage:
raxInsert(rt,(unsigned char*)"mykey",5,some_void_value,NULL);
If the associated value data is NULL, the node where the key is stored does not use additional memory to store the NULL value, so dictionaries composed of just keys are memory efficient if you use NULL as associated value.
Note that keys are unsigned arrays of chars and you need to specify the length: Rax is binary safe, so the key can be anything.
The insertion function is also available in a variant that will not overwrite the existing key value if any:
int raxTryInsert(rax *rax, unsigned char *s, size_t len, void *data,
void **old);
Key lookup
The lookup function is the following:
void *raxFind(rax *rax, unsigned char *s, size_t len);
void *data = raxFind(rax,mykey,mykey_len);
if (data == raxNotFound) return;
printf("Key value is %p\n", data);
Deleting keys
Deleting the key is as you could imagine it, but with the ability to return by reference the value associated to the key we are about to delete:
int raxRemove(rax *rax, unsigned char *s, size_t len, void **old);
The old argument is optional, if passed will be set to the key associated value if the function successfully finds and removes the key.
Iterators
The Rax key space is ordered lexicographically, using the value of the bytes the keys are
composed of in order to decide which key is greater between two keys. If the prefix is the
same, the longer key is considered to be greater.
Rax iterators allow to seek a given element based on different operators and then to navigate the key space calling raxNext() and raxPrev().
The function raxStart never fails and returns no value. Once an iterator is initialized,
it can be sought (sought is the past tens of 'seek', which is not 'seeked',
in case you wonder) in order to start the iteration from the specified position.
For this goal, the function raxSeek is used:
For instance one may want to seek the first element greater or equal to the key "foo":
The function raxSeek() returns 1 on success, or 0 on failure. Possible failures are:
1) An invalid operator was passed as last argument.
2) An out of memory condition happened while seeking the iterator.
Once the iterator is sought, it is possible to iterate using the function raxNext and raxPrev as in the following example:
The function raxNext returns elements starting from the element sought with raxSeek,
till the final element of the tree. When there are no more elements, 0 is returned,
otherwise the function returns 1. However the function may return 0 when an out of memory
condition happens as well: while it attempts to always use the stack, if the tree depth
is large or the keys are big the iterator starts to use heap allocated memory.
The function raxPrev works exactly in the same way, but will move towards the first element of the radix tree instead of moving towards the last element.
Rax iterators allow to seek a given element based on different operators and then to navigate the key space calling raxNext() and raxPrev().
Basic iterator usage
Iterators are normally declared as local variables allocated on the stack, and then initialized with the raxStart function:
raxIterator iter;
raxStart(&iter, rt); // Note that 'rt' is the radix tree pointer.
int raxSeek(raxIterator *it, unsigned char *ele, size_t len, const char *op);
raxSeek(&iter,">=",(unsigned char*)"foo",3);
1) An invalid operator was passed as last argument.
2) An out of memory condition happened while seeking the iterator.
Once the iterator is sought, it is possible to iterate using the function raxNext and raxPrev as in the following example:
while(raxNext(&iter)) {
printf("Key: %.*s\n", (int)iter.key_len, (char*)iter.key);
}
The function raxPrev works exactly in the same way, but will move towards the first element of the radix tree instead of moving towards the last element.
Releasing iterators
An iterator can be used multiple times, and can be sought again and again using raxSeek
without any need to call raxStart again. However, when the iterator is not going to be
used again, its memory must be reclaimed with the following call:
Note that even if you do not call raxStop, most of the times you'll not detect any memory
leak, but this is just a side effect of how the Rax implementation works: most of the times
it will try to use the stack allocated data structures. However for deep trees or large keys,
heap memory will be allocated, and failing to call raxStop will result into a memory leak.
In order to seek the first element >= to the string "foo". However other operators are available. The first set are pretty obvious:
Note how certain times the seek will be impossible, for example when the radix tree contains no elements or when we are asking for a seek that is not possible, like in the following case:
We may not have any element greater than "zzzzz". In this case, what happens is that the
first call to raxNext or raxPrev will simply return zero, so no elements are iterated.
The above code shows a complete range iterator just printing the keys traversed by iterating.
The prototype of the raxCompare function is the following:
The operators supported are >, >=, <, <=, ==. The function returns 1 if the current
iterator key satisfies the operator compared to the provided key, otherwise 0 is returned.
This condition can be tested with the following function that returns 1 if EOF was reached:
Fortunately there is a very simple way to do this, and the efficiency cost is only paid as needed, that is, only when the tree is actually modified. The solution consists of seeking the iterator again, with the current key, once the tree is modified, like in the following example:
In the above case we are iterating with raxNext, so we are going towards lexicographically
greater elements. Every time we remove an element, what we need to do is to seek it again
using the current element and the > seek operator: this way we'll move to the next element
with a new state representing the current radix tree (after the change).
The same idea can be used in different contexts, considering the following:
The simplest way to continue the iteration, starting again from the last element returned by the iterator, is simply to seek itself:
So for example in order to write a command that prints all the elements of a radix tree
from the first to the last, and later again from the last to the first, reusing the same
iterator, it is possible to use the following approach:
1. The radix tree is not larger than expected (for example augmented with information that allows elements ranking).
2. We want the operation to be fast, at worst logarithmic (so things like reservoir sampling are out since it's O(N)).
However a random walk which is long enough, in trees that are more or less balanced, produces acceptable results, is fast, and eventually returns every possible element, even if not with the right probability.
To perform a random walk, just seek an iterator anywhere and call the following function:
If the number of steps is set to 0, the function will perform a number of random walk
steps between 1 and two times the logarithm in base two of the number of elements inside
the tree, which is often enough to get a decent result. Otherwise, you may specify the
exact number of steps to take.
However note that this works well enough for trees with a few elements, but becomes
hard to read for very large trees.
The following is an example of the output raxShow() produces after adding the specified keys and values:
raxStop(&iter);
Seek operators
The function raxSeek can seek different elements based on the operator. For instance in the example above we used the following call:
raxSeek(&iter,">=",(unsigned char*)"foo",3);
- == seek the element exactly equal to the given one.
- > seek the element immediately greater than the given one.
- >= seek the element equal, or immediately greater than the given one.
- < seek the element immediately smaller than the given one.
- <= seek the element equal, or immediately smaller than the given one.
- ^ seek the smallest element of the radix tree.
- $ seek the greatest element of the radix tree.
Note how certain times the seek will be impossible, for example when the radix tree contains no elements or when we are asking for a seek that is not possible, like in the following case:
raxSeek(&iter,">",(unsigned char*)"zzzzz",5);
Iterator stop condition
Sometimes we want to iterate specific ranges, for example from AAA to BBB. In order to do so, we could seek and get the next element. However we need to stop once the returned key is greater than BBB. The Rax library offers the raxCompare function in order to avoid you need to code the same string comparison function again and again based on the exact iteration you are doing:
raxIterator iter;
raxStart(&iter);
raxSeek(&iter,">=",(unsigned char*)"AAA",3); // Seek the first element
while(raxNext(&iter)) {
if (raxCompare(&iter,">",(unsigned char*)"BBB",3)) break;
printf("Current key: %.*s\n", (int)iter.key_len,(char*)iter.key);
}
raxStop(&iter);
The prototype of the raxCompare function is the following:
int raxCompare(raxIterator *iter, const char *op, unsigned char *key, size_t key_len);
Checking for iterator EOF condition
Sometimes we want to know if the itereator is in EOF state before calling raxNext() or raxPrev(). The iterator EOF condition happens when there are no more elements to return via raxNext() or raxPrev() call, because either raxSeek() failed to seek the requested element, or because EOF was reached while navigating the tree with raxPrev() and raxNext() calls.This condition can be tested with the following function that returns 1 if EOF was reached:
int raxEOF(raxIterator *it);
Modifying the radix tree while iterating
In order to be efficient, the Rax iterator caches the exact node we are at, so that at the next iteration step, it can start from where it left. However an iterator has sufficient state in order to re-seek again in case the cached node pointers are no longer valid. This problem happens when we want to modify a radix tree during an iteration. A common pattern is, for instance, deleting all the elements that match a given condition.Fortunately there is a very simple way to do this, and the efficiency cost is only paid as needed, that is, only when the tree is actually modified. The solution consists of seeking the iterator again, with the current key, once the tree is modified, like in the following example:
while(raxNext(&iter,...)) {
if (raxRemove(rax,...)) {
raxSeek(&iter,">",iter.key,iter.key_size);
}
}
The same idea can be used in different contexts, considering the following:
- Iterators need to be sought again with raxSeek every time keys are added or removed while iterating.
- The current iterator key is always valid to access via iter.key_size and iter.key, even after it was deleted from the radix tree.
Re-seeking iterators after EOF
After iteration reaches an EOF condition since there are no more elements to return, because we reached one or the other end of the radix tree, the EOF condition is permanent, and even iterating in the reverse direction will not produce any result.The simplest way to continue the iteration, starting again from the last element returned by the iterator, is simply to seek itself:
raxSeek(&iter,iter.key,iter.key_len,"==");
raxSeek(&iter,"^",NULL,0);
while(raxNext(&iter,NULL,0,NULL))
printf("%.*s\n", (int)iter.key_len, (char*)iter.key);
raxSeek(&iter,"==",iter.key,iter.key_len);
while(raxPrev(&iter,NULL,0,NULL))
printf("%.*s\n", (int)iter.key_len, (char*)iter.key);
Random element selection
To extract a fair element from a radix tree so that every element is returned with the same probability is not possible if we require that:1. The radix tree is not larger than expected (for example augmented with information that allows elements ranking).
2. We want the operation to be fast, at worst logarithmic (so things like reservoir sampling are out since it's O(N)).
However a random walk which is long enough, in trees that are more or less balanced, produces acceptable results, is fast, and eventually returns every possible element, even if not with the right probability.
To perform a random walk, just seek an iterator anywhere and call the following function:
int raxRandomWalk(raxIterator *it, size_t steps);
Printing trees
For debugging purposes, or educational ones, it is possible to use the following call in order to get an ASCII art representation of a radix tree and the nodes it is composed of:
raxShow(mytree);
The following is an example of the output raxShow() produces after adding the specified keys and values:
- alligator = (nil)
- alien = 0x1
- baloon = 0x2
- chromodynamic = 0x3
- romane = 0x4
- romanus = 0x5
- romulus = 0x6
- rubens = 0x7
- ruber = 0x8
- rubicon = 0x9
- rubicundus = 0xa
- all = 0xb
- rub = 0xc
- ba = 0xd
[abcr]
`-(a) [l] -> [il]
`-(i) "en" -> []=0x1
`-(l) "igator"=0xb -> []=(nil)
`-(b) [a] -> "loon"=0xd -> []=0x2
`-(c) "hromodynamic" -> []=0x3
`-(r) [ou]
`-(o) [m] -> [au]
`-(a) [n] -> [eu]
`-(e) []=0x4
`-(u) [s] -> []=0x5
`-(u) "lus" -> []=0x6
`-(u) [b] -> [ei]=0xc
`-(e) [nr]
`-(n) [s] -> []=0x7
`-(r) []=0x8
`-(i) [c] -> [ou]
`-(o) [n] -> []=0x9
`-(u) "ndus" -> []=0xa
Running the Rax tests
To run the tests try:
To run the benchmark:
To test Rax under OOM conditions:
The last one is very verbose currently.
In order to test with Valgrind, just run the tests using it, however if you want accurate leaks detection, let Valgrind run the whole test, since if you stop it earlier it will detect a lot of false positive memory leaks. This is due to the fact that Rax put pointers at unaligned addresses with memcpy, so it is not obvious where pointers are stored for Valgrind, that will detect the leaks. However, at the end of the test, Valgrind will detect that all the allocations were later freed, and will report that there are no leaks.
$ make
$ ./rax-test
$ make
$ ./rax-test --bench
$ make
$ ./rax-oom-test
In order to test with Valgrind, just run the tests using it, however if you want accurate leaks detection, let Valgrind run the whole test, since if you stop it earlier it will detect a lot of false positive memory leaks. This is due to the fact that Rax put pointers at unaligned addresses with memcpy, so it is not obvious where pointers are stored for Valgrind, that will detect the leaks. However, at the end of the test, Valgrind will detect that all the allocations were later freed, and will report that there are no leaks.
do_units: --units
- randomWalkTest:
- iteratorUnitTests: raxSeek() 테스트
- tryInsertUnitTests: raxInsert(), raxTryInsert() 테스트
do_regression: --regression
- regtest1:
- regtest2:
- regtest3:
- regtest4:
- regtest5:
- regtest6:
do_hugekey: --hugekey
- testHugeKey:
do_fuzz_cluster: --fuzz-cluster
- fuzzTestCluster:
do_fuzz: --fuzz
- uzzTest(KEY_INT):
- uzzTest(KEY_UNIQUE_ALPHA):
- uzzTest(KEY_RANDOM):
- uzzTest(KEY_RANDOM_ALPHA):
- uzzTest(KEY_RANDOM_SMALL_CSET):
- uzzTest(KEY_CHAIN):
- iteratorFuzzTest(KEY_CHAIN):
- iteratorFuzzTest(KEY_UNIQUE_ALPHA):
- iteratorFuzzTest(KEY_RANDOM_ALPHA):
- iteratorFuzzTest(KEY_RANDOM):
do_benchmark: --bench
- benchmark():
Debugging Rax
While investigating problems in Rax it is possible to turn debugging messages on by
compiling with the macro RAX_DEBUG_MSG enabled. Note that it's a lot of output,
and may make running large tests too slow.
In order to active debugging selectively in a dynamic way, it is possible to use the function raxSetDebugMsg(0) or raxSetDebugMsg(1) to disable/enable debugging.
A problem when debugging code doing complex memory operations like a radix tree implemented the way Rax is implemented, is to understand where the bug happens (for instance a memory corruption). For that goal it is possible to use the function raxTouch() that will basically recursively access every node in the radix tree, itearting every sub child. In combination with tools like Valgrind, it is possible then to perform the following pattern in order to narrow down the state causing a give bug:
In order to active debugging selectively in a dynamic way, it is possible to use the function raxSetDebugMsg(0) or raxSetDebugMsg(1) to disable/enable debugging.
A problem when debugging code doing complex memory operations like a radix tree implemented the way Rax is implemented, is to understand where the bug happens (for instance a memory corruption). For that goal it is possible to use the function raxTouch() that will basically recursively access every node in the radix tree, itearting every sub child. In combination with tools like Valgrind, it is possible then to perform the following pattern in order to narrow down the state causing a give bug:
- The rax-test is executed using Valgrind, adding a printf() so that for the fuzz tester we see what iteration in the loop we are in.
- After every modification of the radix tree made by the fuzz tester in rax-test.c, we add a call to raxTouch().
- Now as soon as an operation will corrupt the tree, raxTouch() will detect it (via Valgrind) immediately. We can add more calls to narrow the state.
- At this point a good idea is to enable Rax debugging messages immediately before the moment the tree is corrupted, to see what happens. This can be achieved by adding a few "if" statements inside the code, since we know the iteration that causes the corruption (because of step 1).
| << HASH Table of HASHES | RAX Radix Tree | Listpack >> |
|---|
조회수 :
Email
답글이 올라오면 이메일로 알려드리겠습니다.